Nastro di Moebius: significato e video

Nastro di Moebius, un trucco da maghi, un rompicapo, una creatura matematica e geometrica che lascia sempre a bocca aperta ogni volta che lo si osserva per la prima volta. E anche dopo. In matematica, e più precisamente in topologia, il nastro di Mobius, è molto noto come esempio di superficie non orientabile e di superficie rigata. Il suo creatore, gli ha donato anche il nome, ed è il matematico tedesco August Ferdinand Möbius.

Nastro di Moebius: significato

Perché questo nastro è così noto, studiato e ritratto? Perché non è un nastro comune. Quello comuni, visti come superfici, in senso matematico, sono superfici che, come tutte le altre, hanno sempre due facce. Se camminiamo su una faccia, non possiamo ritrovarci a farlo sull’altra.

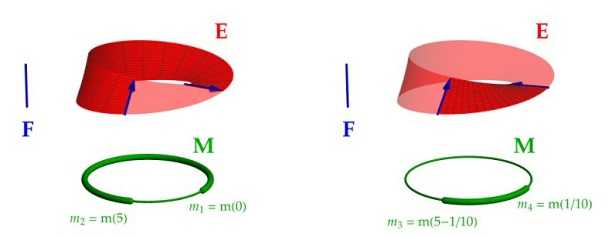
Non è possibile, a meno che non si attraversi un suo spigolo, un bordo, una qual si voglia superficie di demarcazione. E’ ciò che avviene ad esempio alla sfera, al toro, o al cilindro, superfici di cui è possibile stabilire convenzionalmente un lato “superiore” o “inferiore”, oppure “interno” o “esterno”. L’interno del Nastro di Moebius non esiste, o meglio, non è distinguibile dal suo esterno.

Nastro di Moebius: video

Se la situazione sembra confusa, con questo video, le cose migliorano e il Nastro di Moebius vi parrà qualcosa di più concreto.

Nastro di Moebius: filosofia

Dietro al Nastro di Moebius, non c’è solo matematica, ma anche molta filosofia. Potete immaginare anche voi che riflessioni può fare nascere una superficie che non ha interno ed esterno, che possiamo percorrere all’infinito senza mai capire su quale delle sue parti stiamo camminando. L’infinito, l’interno e l’esterno, l’idea di un bordo o di una linea da varcare, sono tutti concetti che ancora oggi i filosofi affrontano scontrandosi.

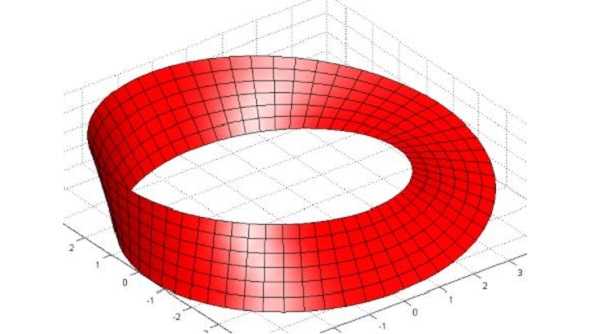
Nastro di Moebius: come realizzarlo

Prendiamo una striscia rettangolare di carta e uniamone i lati corti dopo aver impresso ad uno di essi una torsione di 180°. Con una matita o un pennarello percorriamo il nastro da un punto a caso, avanzando. La striscia che otteniamo si snoda sull’intera superficie del nastro, che è quindi unica. Proprio come detto. Non abbiamo dovuto staccare il pennarello dalla carta per tracciarla e abbiamo colorato su tutto il Nastro di Moebius perché di fatto esiste un solo lato e un solo bordo. Costruire questo nastro è utile per la mente come fare esercizi per la memoria

Il matematico August Ferdinand Möbius è stato il primo a tutti gli effetti a considerare la possibilità di realizzare figure topologiche non orientabili. Anche se possiamo venire ingannati dalla somiglianza, va chiarito che il simbolo matematico ∞ di infinito non fa riferimento al nastro ma lo ha introdotto in circostanze del tutto diverse il matematico inglese John Wallis. 

Per chi volesse lanciarsi in una impresa impossibile, ecco la bottiglia di Klein che anche con tutto l’impegno, è ben difficile da tradurre in oggetto tangibile pur restando una superficie molto affascinante

Nastro di Moebius: architettura

In architettura questo nastro ha ovviamente fatto sbizzarrire molti che per ovvi motivi hanno preso ispirazione da questa figura per realizzare edifici spaziosi ed enigmatici. Anche la moda ha colto l’occasione soprattutto utilizzandolo come simbolo, come sulla maglia dedicata in 100% cotone, acquistabile anche su Amazon in vari colori.

Nastro di Moebius: film

Può capitare che, cercando il Nastro, ci si trovi di fronte ad un film che poco ha a che fare con la matematica e la geometria. Il film si chiama solo “Moebius”, è’ la latinizzazione riveduta della lingua coreana: Moibi-useu, letteralmente “nastro di Möbius“. Il film è diretto da Kim Ki-duk, è privo di dialoghi ed è stato presentato fuori concorso al Festival di Venezia 2013.

Se vi è piaciuto questo articolo continuate a seguirmi anche su Twitter, Facebook, Google+, Instagram

Pubblicato da Marta Abbà il 30 Marzo 2018