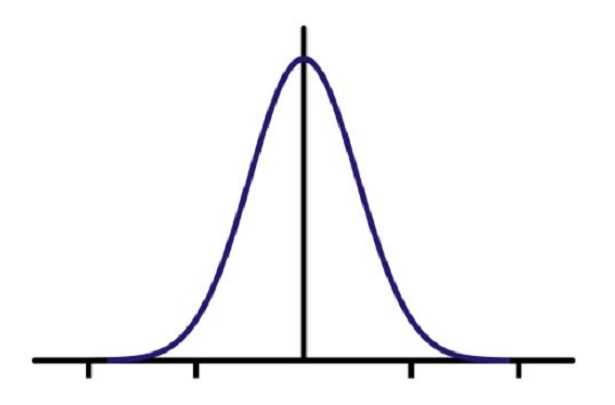
Curva gaussiana e Curva di distribuzione
Curva gaussiana, un concetto matematico ma affatto sconnesso dalla realtà perché in grado di rappresentare molte situazioni quotidiane semplificandone l’interpretazione. Vediamo quindi di cosa si tratta e cosa racconta di quel che ci accade attorno. La troviamo disegnata in un piano di coordinate cartesiane ma anche come distribuzione o come superficie.
Curva gaussiana
La Gaussiana, o curva di Gauss, è stata “inventata” dal matematico tedesco Karl Friedrich Gauss. Le sue formule e tutto ciò che di matematico ci sta dietro, è noto a pochi, ma il suo significato generale e la sua utilità è nota a molti.
Curva gaussiana e distribuzione
Quando tracciamo una curva gaussiana proviamo a rappresentare un certo evento rappresentando in modo grafico la distribuzione dei suoi possibili valori. Prendiamo l’esito del lancio una moneta oppure qualcosa di più complesso come le persone che tifano una certa squadra divise per fasce di età.
Per ottenere la distribuzione gaussiana di un valore che stiamo misurando, bisogna effettuare tante misurazioni di una stessa grandezza con uno strumento raccogliendo i vari risultati. Non si otterrà sempre lo stesso numero per via degli errori di precisione del nostro strumento e anche per quelli legati al nostro operato, detti errori accidentali. Più sono numerose le nostre misure, più la loro rappresentazione su un grafico sarà una curva gaussiana.
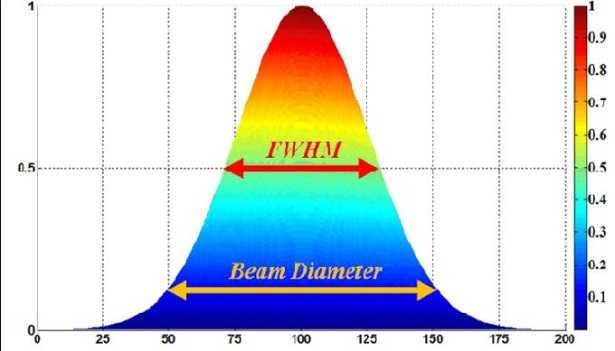
Curva gaussiana e tabella
In accompagnamento ad una curva gaussiana possiamo trovare anche una tabella con i valori che corrispondono ai vari punti nel piano rappresentati e uniti. Guardando la curva gaussiana e la tabella, vediamo che c’è un punto massimo della “campana” che poi scende in modo più o meno evidente.
Dipende dalla dispersione dei valori attorno alla media che si misura con la deviazione standard. Tabella alla mano, possiamo dire che per la curva gaussiana o il 68% delle misurazioni differisce dalla media meno della deviazione standard e che il 95% mendi due deviazioni standard. Se la deviazione standard quindi ha un valore alto, avremo una campana, quindi una gaussiana che scende più morbidamente prima e dopo il suo massimo e il massimo, a questo punto, corrisponde ad un valore sì più probabile ma non sempre rappresentativo.
Dato che si parla di probabilità di ottenere un certo valore, anche per la curva gaussiana, vale che l’area ad essa sottesa vale 1. La somma delle probabilità di tutti i valori deve dare 1.
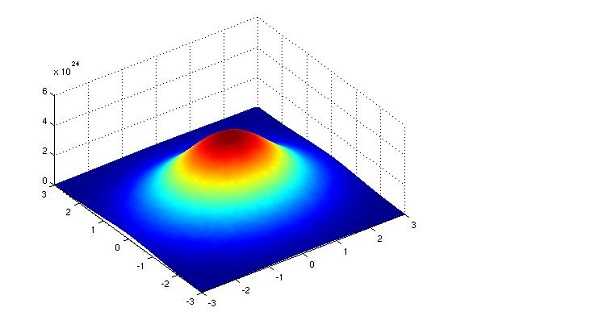
Curva gaussiana e superficie
La superficie gaussiana è un concetto legato alla legge di Gauss. Nello specifico, dato un campo elettrico, per individuare la superficie gaussiana è necessario trovare in uno spazio a tre dimensioni la superficie normale al campo elettrico in ciascun punto. Chiusa nello spazio a tre dimensioni, attraversata da un flusso di campo elettrico, tale superficie può anche essere semplicemente una sfera o un cilindro infinito. Ciò accade rispettivamente quando il campo che consideriamo, viene prodotto da una carica puntiforme e da un filo conduttore di lunghezza infinita.
Curva gaussiana e funzione
Inoltrandoci sempre di più nel campo della fisica e della matematica, troviamo anche le funzioni gaussiane in cui integrale è la funzione degli errori. Qualche esempio di funzione gaussiana, anzi, uno per tutti: la funzione d’onda dello stato fondamentale dell’oscillatore armonico quantistico. Motivo per cui sentiamo parlare di funzioni gaussiane nella teoria quantistica dei campi.
Se vi è piaciuto questo articolo continuate a seguirmi anche su Twitter, Facebook, Google+, Instagram
Ti potrebbe interessare anche:
- Istogramma: significato
- Geometria euclidea e non
- Curva di indifferenza
- Diagrammi di flusso
- Diagramma di Venn
Pubblicato da Marta Abbà il 19 Febbraio 2018
